
Change prompt
from octave:1>` to `>>
octave:1> PS1('>> ');
>> Help command
>> help help
'help' is a function from the file C:\Octave\OCTAVE~1.0\mingw64\share\octave\5.2.0\m\help\help.m
-- help NAME
-- help --list
-- help .
-- help
Display the help text for NAME.
For example, the command 'help help' prints a short message
describing the 'help' command.
Given the single argument '--list', list all operators, keywords,
built-in functions, and loadable functions available in the current
session of Octave.
Given the single argument '.', list all operators available in the
current session of Octave.
If invoked without any arguments, 'help' displays instructions on
how to access help from the command line.
The help command can provide information about most operators, but
NAME must be enclosed by single or double quotes to prevent the
Octave interpreter from acting on NAME. For example, 'help "+"'
displays help on the addition operator.
See also: doc, lookfor, which, info.
Additional help for built-in functions and operators is
available in the online version of the manual. Use the command
'doc <topic>' to search the manual index.
Help and information about Octave is also available on the WWW
at https://www.octave.org and via the help@octave.org
mailing list.Basic Operations
Math Operations
Addition
>> 5+6
ans = 11Subtraction
>> 3-2
ans = 1Multiplication
>> 5*8
ans = 40Division
>> 1/2
ans = 0.50000Exponent
>> 2^6
ans = 64Logic operations
Equality
>> 1 == 2
ans = 0Inequality
>> 1 ~= 2
ans = 1Logical AND
>> 1 && 0
ans = 0Logical OR
>> 1 || 0
ans = 1Logical XOR
>> xor(1,0)
ans = 1 Variables
Assignments
numbers
>> a =3;
>> a
a = 3strings
>> b = 'hi';
>> b
b = 'hi'calculations
>> c = (3>=1);
>> c
c = 1$\pi$
>> a = pi;
>> a
>> a = 3.1416Displaying Variables
numbers
>> a = pi;
>> disp(a)
3.1416strings
>> a = pi;
>> disp(sprintf('2 decimals: %0.2f', a));
2 decimals: 3.14
>> disp(sprintf('6 decimals: %0.6f', a));
6 decimals: 3.141593format
>> a = pi;
>> format long
>> a
a = 3.14159165358979
>> format short
>> a
a = 3.1416Matrices
3×2 matrix
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6or
>> A = [1 2;
> 3 4;
> 5 6]
A =
1 2
3 4
5 61×3 Matrix
>> V = [1 2 3 ]
V =
1 2 33×1 Vector
>> V = [1; 2; 3;]
V =
1
2
3Creating vector from 1 to 2 increasing next element by 0.1
>> V = 1:0.1:2
V =
1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000Creating vector from 1 to 6 increasing next element by 1
>> V = 1:6
V =
1 2 3 4 5 6Matrix 2×3 with all values eqauls 1
>> ones(2,3)
ans =
1 1 1
1 1 1Matrix 2×3 with all values eqauls 2
>> C = 2*ones(2,3)
C =
2 2 2
2 2 2Row vector with 1
>> w = ones(1,3)
w =
1 1 1Row vector with 0
>> w = zeros(1,3)
w =
0 0 0Random matrix (numbers between 0 and 1)
>> rand(1,3)
ans =
0.32784 0.49321 0.17449
>> rand(3,3)
ans =
0.60369 0.15891 0.75957
0.47148 0.11786 0.86370
0.46272 0.51486 0.71124Gaussian random variables
>> randn(1,3)
ans =
-0.67605 -0.54028 0.42763
More complicated
>> w = -6 + sqrt(10)*randn(1,100)
w =
Columns 1 through 8:
-4.5865653 -8.8356479 -8.1333614 -2.3439273 -7.3621630 -9.0450181 -2.1489934 -4.2785162
Columns 9 through 16:
-10.7109066 -7.5124041 -6.6674847 -14.4887638 -0.4808289 -2.1354753 -7.8977581 -8.9314986
Columns 17 through 24:
-8.9893458 -1.5510572 -10.3796268 -10.2004881 -1.9258233 -10.7401729 -1.4114864 -11.9918739
Columns 25 through 32:
-1.4288672 -9.1350859 -4.0339111 -7.1057222 -5.5066692 -5.3943613 -9.9372854 -12.3273985
Columns 33 through 40:
-9.1448272 -3.5632437 -9.8825123 -3.6862963 -0.9314631 -7.1585643 -7.5249914 -6.7338681
Columns 41 through 48:
-4.0692604 -3.1736484 -7.1340077 -5.6141781 -7.1375287 -10.1554003 -7.3884758 -8.2993959
Columns 49 through 56:
-7.9971092 -3.7486347 -4.9565946 -10.1077235 -3.7186839 -7.6239998 -9.3567788 -7.0285528
Columns 57 through 64:
-5.7498064 -5.1235503 2.6385315 -7.0795552 -5.1845500 -2.7447164 -7.7785950 0.8816560
Columns 65 through 72:
-6.5335031 0.0066014 -3.9586199 -2.1445580 -3.4484948 -12.8979017 -1.5233025 -4.4102424
Columns 73 through 80:
0.9831482 -4.7574813 -2.7595514 -11.2178766 -5.3229671 -1.8543523 -3.7577500 -3.8678680
Columns 81 through 88:
-3.8637871 -7.2037168 -11.7877396 -7.1542280 -7.5999564 0.2206099 -6.7140798 -1.3302397
Columns 89 through 96:
-3.6058713 -5.5103303 -5.8951690 -1.6396029 -8.2389941 -4.5821969 -4.4162341 -6.9883700
Columns 97 through 100:
-3.4562746 -3.8389149 -0.8080181 -4.6449049
```
#### Histagram
```r
>> hist(w)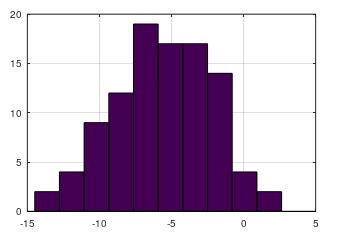
>> hist(w,50)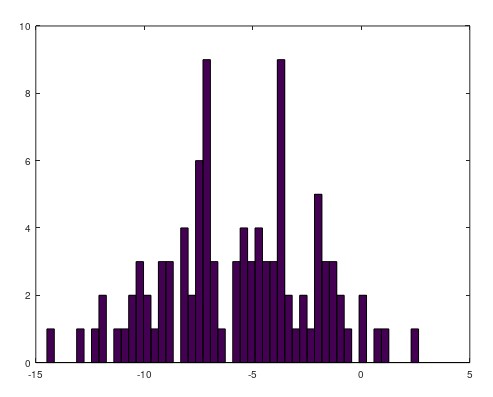
>> eye(4)
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Moving Data Around
Matrices size
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> size(A)
ans =
3 2Get dimensions (rows) of Matrix
>> size(A,1)
ans = 3Get number of columns
>> size(A,2)
ans = 2Length of Vector
V =
4 3 1 5
>> length(V)
ans = 4It can be applied as well to Matrices, but then the result will be only for the longest dimension
>> length(A)
ans = 3Loading data
Show the current directory
>> pwd
ans = C:\Users\GosiaChanging directory
>> cd 'D:\Projects'
>> pwd
ans = D:\ProjectsLoad data
>> load data.txtdisplay data from the file
>> data
data =
6.11010 17.59200
5.52770 9.13020
8.51860 13.66200
7.00320 11.85400
5.85980 6.82330
8.38290 11.88600
7.47640 4.34830
8.57810 12.00000
6.48620 6.59870
5.05460 3.81660
5.71070 3.25220
14.16400 15.50500
5.73400 3.15510
8.40840 7.22580
5.64070 0.71618
5.37940 3.51290
6.36540 5.30480
5.13010 0.56077
6.42960 3.65180
7.07080 5.38930
6.18910 3.13860check the size of data (file)
>> size(data)
ans =
97 2check variables that Octave has in memory
>> who
Variables in the current scope:
A V a ans b c data wcheck variables with details that Octave has in memory
>> whos
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
A 3x2 48 double
V 1x4 32 double
a 1x1 8 double
ans 1x2 16 double
b 1x2 2 char
c 1x1 1 logical
data 97x2 1552 double
w 1x100 800 double
Total is 310 elements using 2459 bytesassign only selected data from one variable to another
>> m = data(1:10)
m =
6.1101 5.5277 8.5186 7.0032 5.8598 8.3829 7.4764 8.5781 6.4862 5.0546
>> whos
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
A 3x2 48 double
V 1x4 32 double
a 1x1 8 double
ans 1x2 16 double
b 1x2 2 char
c 1x1 1 logical
data 97x2 1552 double
m 1x10 80 double
w 1x100 800 double
Total is 320 elements using 2539 bytessave a variable to a file (in binary format)
>> save hello.mat m;
>> ls
Volume in drive D is Data
Volume Serial Number is 9C15-10B4
Directory of D:\machine-learning-ex\test
[.] [..] data.txt hello.mat
2 File(s) 1,691 bytes
2 Dir(s) 88,129,142,784 bytes freesave a variable to a file (in ascii format)
>> save hello.txt m -asciihello.txt
6.11010000e+00 5.52770000e+00 8.51860000e+00 7.00320000e+00 5.85980000e+00 8.38290000e+00 7.47640000e+00 8.57810000e+00 6.48620000e+00 5.05460000e+00clear selected variable
>> clear data
>> whos
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
A 3x2 48 double
V 1x4 32 double
a 1x1 8 double
ans 1x2 16 double
b 1x2 2 char
c 1x1 1 logical
w 1x100 800 double
Total is 116 elements using 907 bytesclear all variables
>> clear
>> whos
>>loading saved variable
>> load hello.mat
>> whos
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
m 1x10 80 double
Total is 10 elements using 80 bytesGet specific element from the variable (example: 3rd column and 2nd row)
>> A=[1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A(3,2)
ans = 6Get everything in a second row
>> A(2,:)
ans =
3 4Get everything in a second column
>> A(:,2)
ans =
2
4
6
Get all elements from specific columns
>> A([1 3],:)
ans =
1 2
5 6
>> A([2 3],:)
ans =
3 4
5 6
>> A([1 2 3],:)
ans =
1 2
3 4
5 6Change data in matrix
>> A
A =
1 2
3 4
5 6
>> A(:,2) = [10;11;12]
A =
1 10
3 11
5 12Add (append) another column vector data to the right
>> A = [A, [100; 101; 102]];
>> A
A =
1 10 100
3 11 101
5 12 102
Put all element of matrix into single column vector
>> A(:)
ans =
1
3
5
10
11
12
100
101
102
Combine two matrices
>> A = [1 2; 3 4; 5 6];
>> B = [11 12; 13 14; 15 16];
>> C = [A B]
C =
1 2 11 12
3 4 13 14
5 6 15 16or
>> A = [1 2; 3 4; 5 6];
>> B = [11 12; 13 14; 15 16];
>> C = [A; B]
C =
1 2
3 4
5 6
11 12
13 14
15 16
Computing on Data
Multiply
>> A = [1 2; 3 4; 5 6];
>> C = [1 1; 2 2];
>> A*C
ans =
5 5
11 11
17 17
Element-wise multiplication
>> A = [1 2; 3 4; 5 6];
>> B = [11 12; 13 14; 15 16];
>> A .*B
ans =
11 24
39 56
75 96
Element-wise squaring
>> A = [1 2; 3 4; 5 6];
>> A .^ 2
ans =
1 4
9 16
25 36
Element-wise Reciprocal
>> V = [1; 2; 3];
>> 1 ./ V
ans =
1.00000
0.50000
0.33333
Element-wise inverse of A (matrix)
>> A = [1 2; 3 4; 5 6];
>> 1 ./A
ans =
1.00000 0.50000
0.33333 0.25000
0.20000 0.16667Element-wise logarithm
>> V = [1; 2; 3];
>> log(V)
ans =
0.00000
0.69315
1.09861Exponentiation
>> V = [1; 2; 3];
>> exp(V)
ans =
2.7183
7.3891
20.0855Element-wise absolute value
>> V = [1; 2; 3];
>> abs(V)
ans =
1
2
3
>> abs([-1; -3; -10])
ans =
1
3
10
negative
>> V = [1; 2; 3];
>> -V
ans =
-1
-2
-3
or
>> V = [1; 2; 3];
>> -1*V
ans =
-1
-2
-3Increment all values by one
>> V = [1; 2; 3];
>> V + ones(length(V),1)
ans =
2
3
4
or
>> V = [1; 2; 3];
>> V + 1
ans =
2
3
4
Matrix transport
>> A = [1 2; 3 4; 5 6];
>> A'
ans =
1 3 5
2 4 6Max value
>> a = [1 15 2 0.5];
>> max(a)
ans = 15Max value and index of this max value
>> val = max(a)
val = 15
>> [val, ind] = max(a)
val = 15
ind = 2Column-wise maximum (on matrices)
>> A = [1 2; 3 4; 5 6];
>> max(A)
ans =
5 6
or
>> A = [1 2; 3 4; 5 6];
>> max(A,[],1)
ans =
5 6
Row-wise maximum (on matrices)
>> A = [1 2; 3 4; 5 6];
>> max(A,[],2)
ans =
2
4
6
The max element in whole matrix
>> A = [1 2; 3 4; 5 6];
>> max(max(A))
ans = 6
or turn into vector
>> A = [1 2; 3 4; 5 6];
>> max(A(:))
ans = 6Element-wise comparison (showing true/false)
>> a = [1 15 2 0.5];
>> a < 3
ans =
1 0 1 1Element-wise comparison (showing with element)
>> a = [1 15 2 0.5];
>> find(a < 3)
ans =
1 3 4Magic (N-by-N magic square)
>> A = magic(3)
A =
8 1 6
3 5 7
4 9 2>> A = magic(9)
A =
47 58 69 80 1 12 23 34 45
57 68 79 9 11 22 33 44 46
67 78 8 10 21 32 43 54 56
77 7 18 20 31 42 53 55 66
6 17 19 30 41 52 63 65 76
16 27 29 40 51 62 64 75 5
26 28 39 50 61 72 74 4 15
36 38 49 60 71 73 3 14 25
37 48 59 70 81 2 13 24 35sum columns
>> sum(A,1)
ans =
369 369 369 369 369 369 369 369 369sum rows
>> sum(A,2)
ans =
369
369
369
369
369
369
369
369
369sum diagonal
>> eye(9)
ans =
Diagonal Matrix
1 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1
>> A .* eye(9)
ans =
47 0 0 0 0 0 0 0 0
0 68 0 0 0 0 0 0 0
0 0 8 0 0 0 0 0 0
0 0 0 20 0 0 0 0 0
0 0 0 0 41 0 0 0 0
0 0 0 0 0 62 0 0 0
0 0 0 0 0 0 74 0 0
0 0 0 0 0 0 0 14 0
0 0 0 0 0 0 0 0 35
>> sum(sum(A.*eye(9)))
ans = 369
>> flipud(eye(9))
ans =
Permutation Matrix
0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 1 0 0
0 0 0 0 0 1 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 1 0 0 0 0 0
0 0 1 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0
>> sum(sum(A.*flipud(eye(9))))
ans = 369finding by row and column
>> A = magic(3);
>> [r,c] = find(A >= 7)
r =
1
3
2
c =
1
2
3
>> [row,column] = find(A >= 7)
row =
1
3
2
column =
1
2
3Pseudo-inverse
>> A = magic(3)
A =
8 1 6
3 5 7
4 9 2
>> pinv(A)
ans =
0.147222 -0.144444 0.063889
-0.061111 0.022222 0.105556
-0.019444 0.188889 -0.102778Add all elements
>> a = [1 15 2 0.5];
>> sum(a)
ans = 18.500Multiply all elements
>> a = [1 15 2 0.5];
>> prod(a)
ans = 15Rounds down elements ( Return the largest integer not greater than X)
>> a = [1 15 2 0.5];
>> floor(a)
ans =
1 15 2 0Rounds up elements ( Return the smallest integer not less than X)
>> a = [1 15 2 0.5];
>> ceil(a)
ans =
1 15 2 1Plotting Data
Sample generated data for the plot (numbers from 0 to up 0.98) and sin function
>> t=[0:0.01:0.98];
>> y1 = sin(2*pi*4*t);Generating plot, where horizontal axis = t and verical axis = y1:
>> plot(t,y1);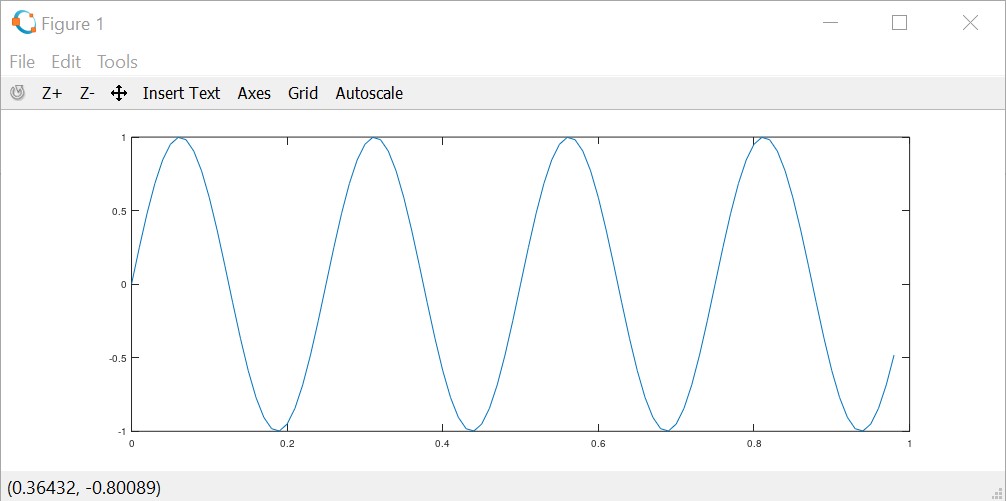
When run once again the plot with different argument, it will be replaced with new plot:
>> y2 = cos(2*pi*4*t);
>> plot(t,y2);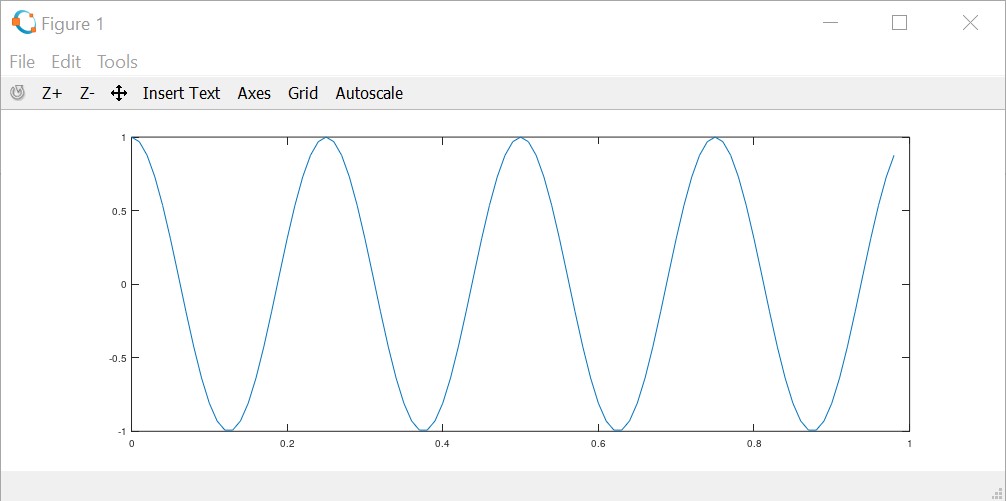
To have both (or more) plots on one designer it's needed to use the ```hold on;``` function:
>> plot(t,y1);
>> hold on;
>> plot(t,y2);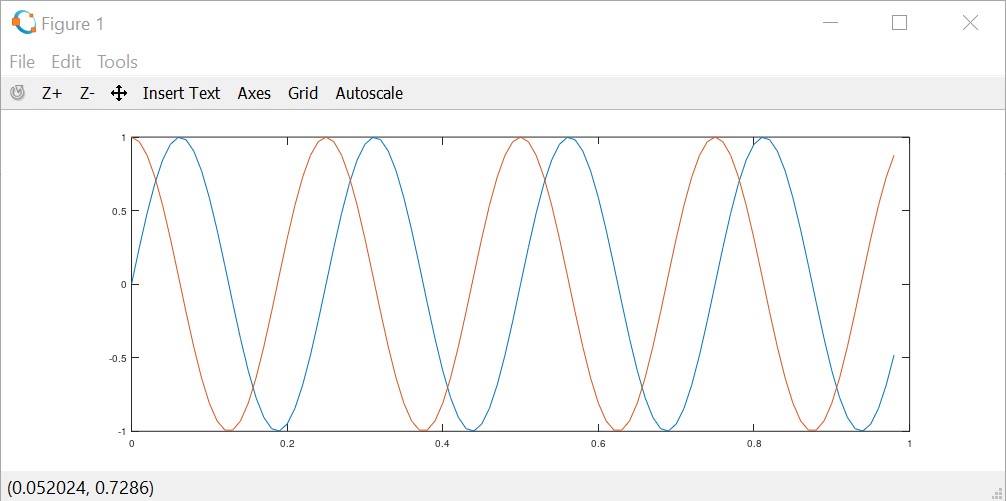
Adding labels, legend and title
>> xlabel('time');
>> ylabel('value');
>> legend('sin','cos');
>> title('my plot');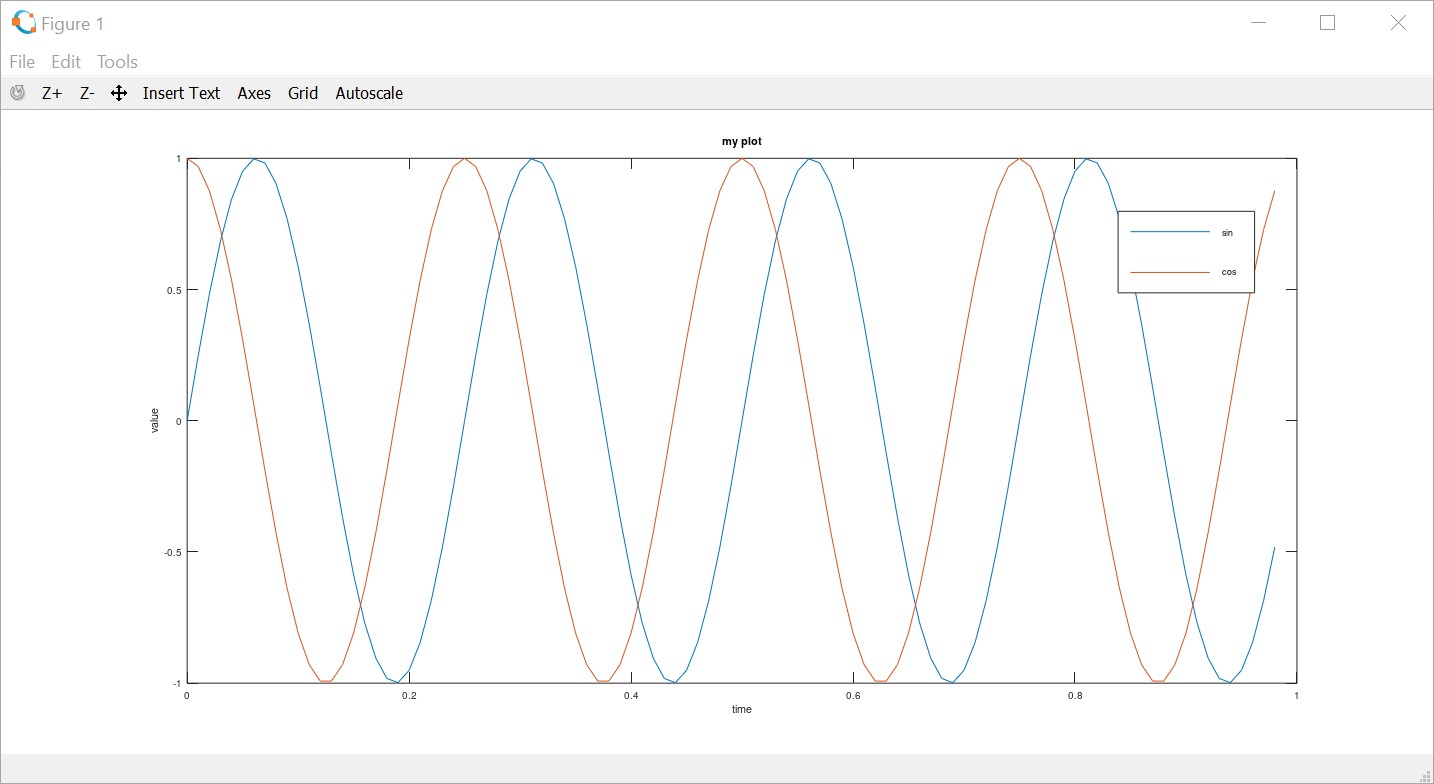
Saving the figure
>> cd D:\; print -dpng 'myPlot.png'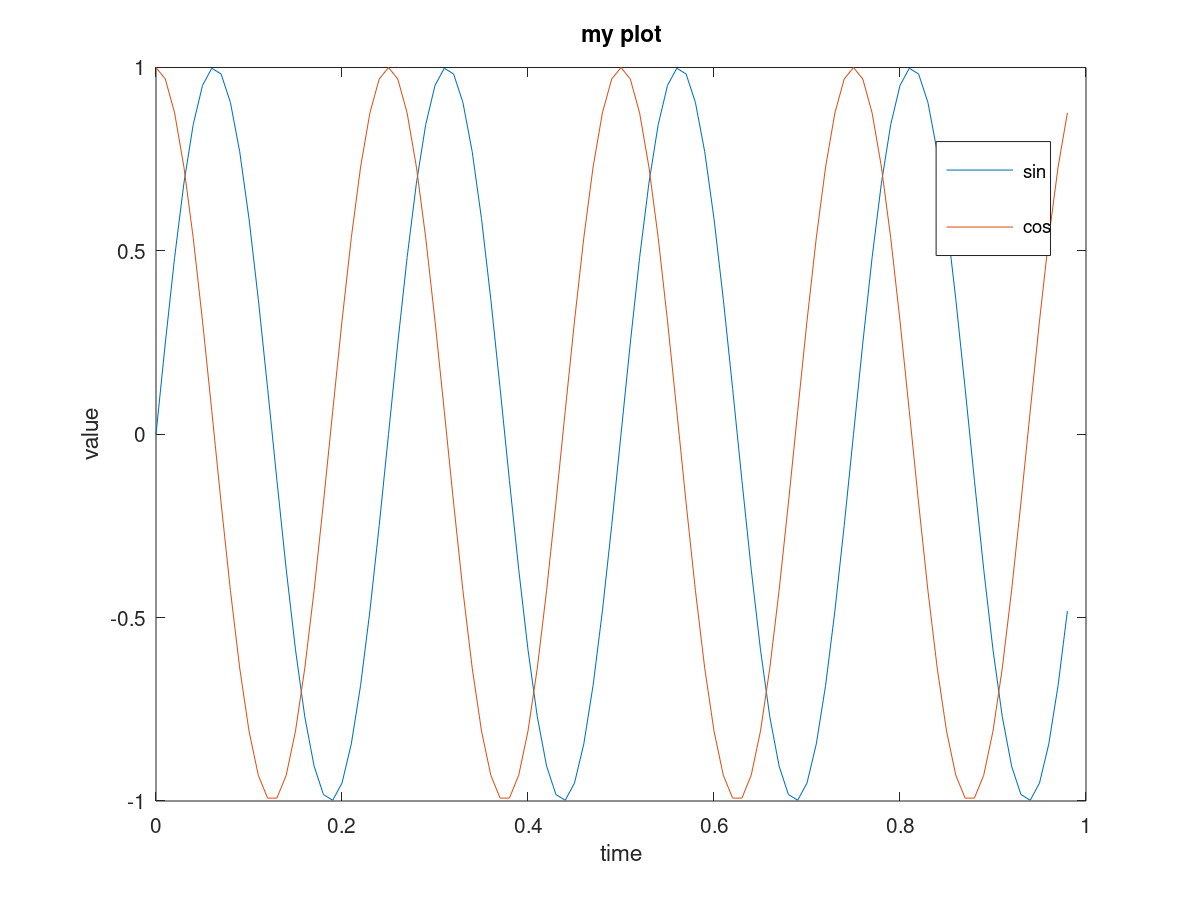
To close figure
>> close;To open two figures in seperate windows:
>> figure(1); plot(t,y1);
>> figure(2); plot(t,y2);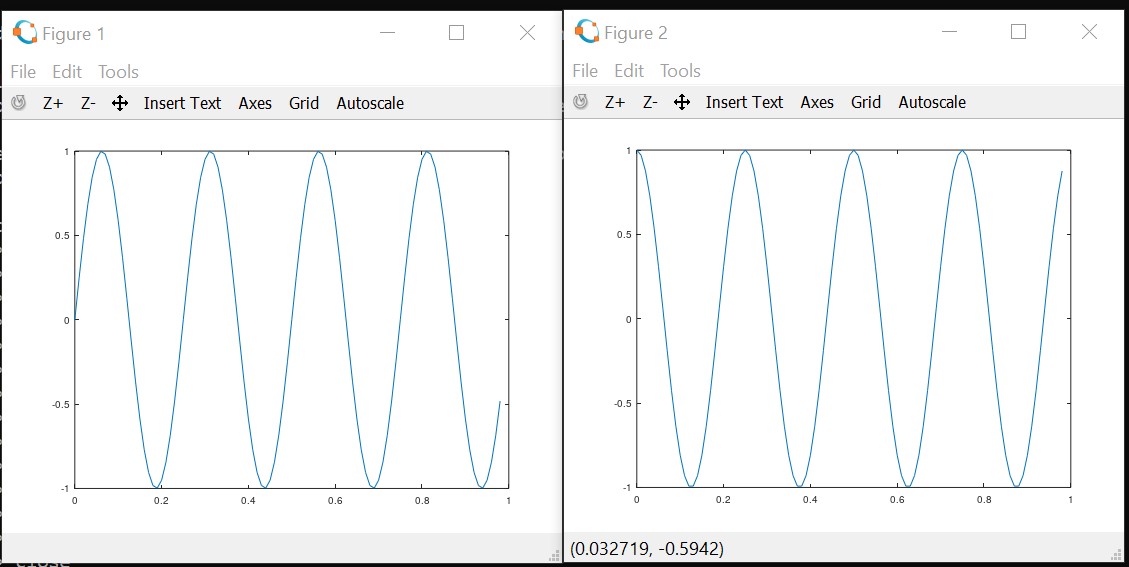
Dividing plot by 1x2 grid and access first element and next second element
>> subplot(1,2,1);
>> plot(t,y1);
Clear figure
>> clf;Visualize matrix
>> A = magic(5)
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> imagesc(A)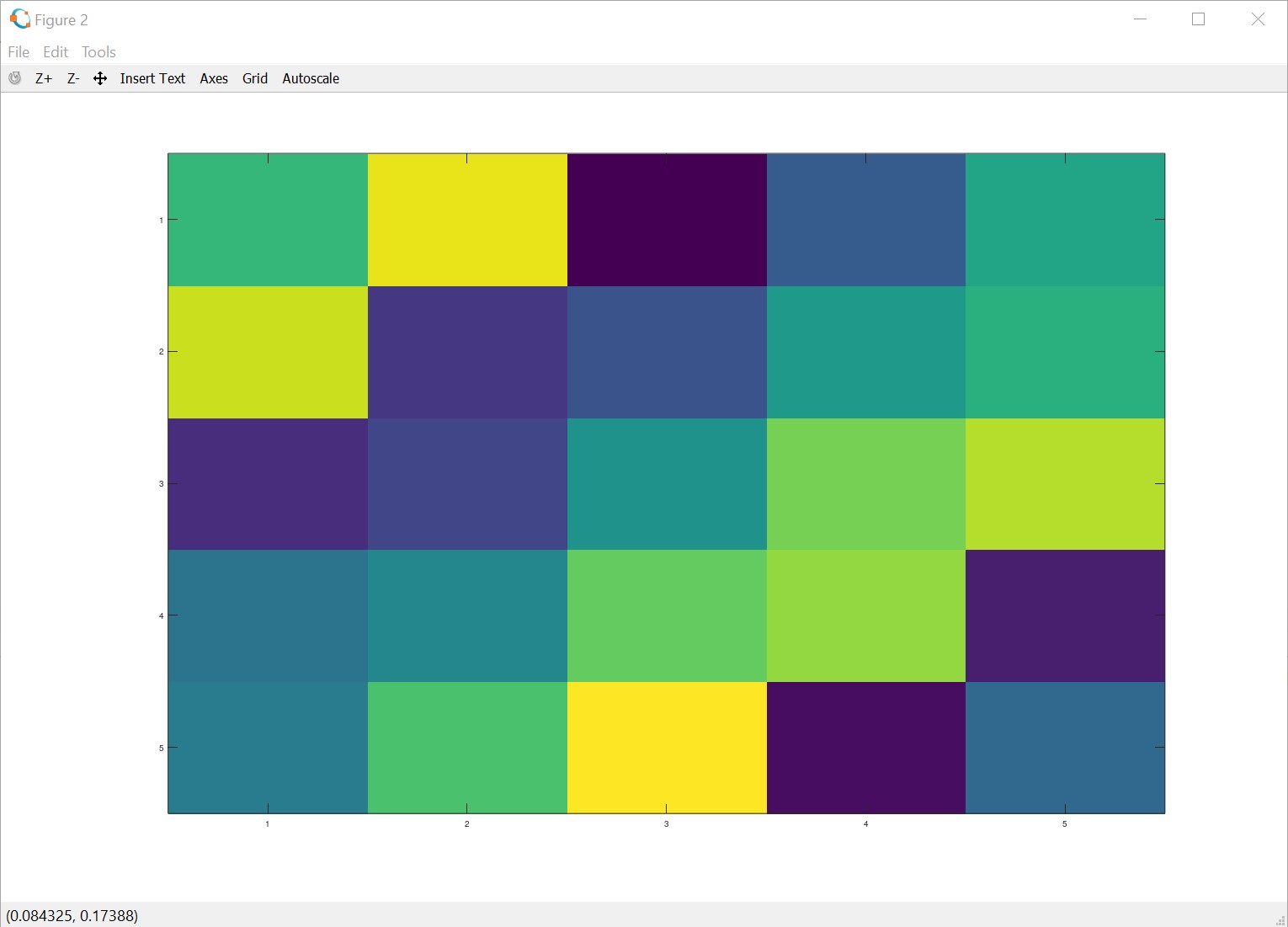
To show with grey colour with colour bar
>> imagesc(A), colorbar, colormap gray;
